A connection of two or more elements is called a node. An example of a node is depicted in the partial circuit shown below:
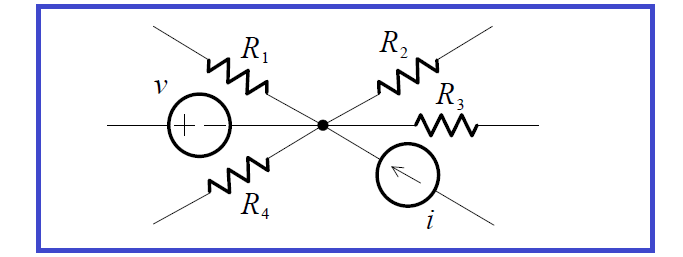
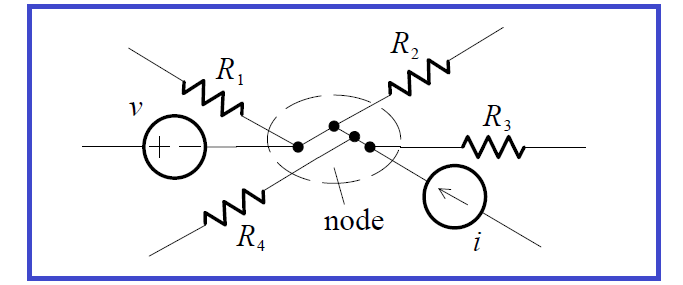
Even if the figure is redrawn to make it appear that there may be more than one node, as in the figure below, the connection of the six elements actually constitutes only one node.
Kirchhoff’s Current Law (KCL) is essentially the law of conservation of electric charge. If currents directed out of a node are positive in sense, and currents directed into a node are negative in sense (or vice versa), then KCL can be stated as follows:
KCL defined
KCL: At any node of a circuit, the currents algebraically sum to zero.
If there are n elements attached to a node then, in symbols, KCL is:

KCL can also be stated as: The sum of the currents entering a node is equal to the sum of the currents leaving a node.
Now we will discuss about KCL law with practical examples below:
Example 1
As an example of KCL, consider a portion of some circuit, shown below:

Choosing the positive sense to be leaving, we apply KCL at the node and obtain the equation:
– i1 + i2 + i3 – i4 + i5 – i6 = 0
Note that even if one of the elements – the one which carries i3– is a short circuit, KCL holds. In other words, KCL applies regardless of the nature of the elements in the circuit.
Example 2
We want to find the voltage v, in the two-node circuit shown below:
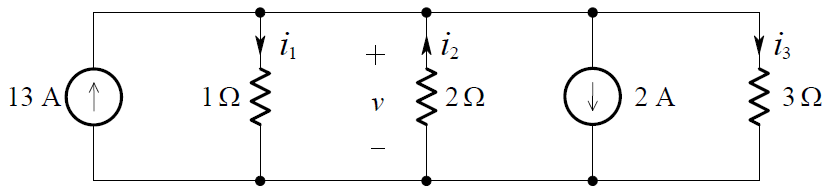
The directions of i1 , i2 , i3 and the polarity of v were chosen arbitrarily (the directions of the 13 A and 2 A sources are given). By KCL (at either of the two nodes), we have:
– 13 + i1 – i2 + 2 + i3 = 0
From this we can write:
i1 – i2 + i3 = 11
By Ohm’s Law:
![]()
Substituting these into the previous equation yields:
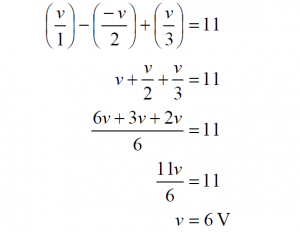
Having solved for v, we can now find that:
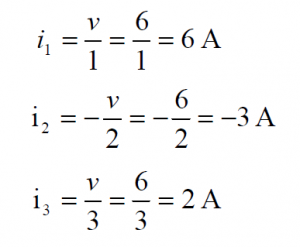
Just as KCL applies to any node of a circuit, so must KCL hold for any closed region, i.e. to satisfy the physical law of conservation of charge, the total current leaving (or entering) a region must be zero.
Example 3
In the circuit shown below, three regions have been identified:
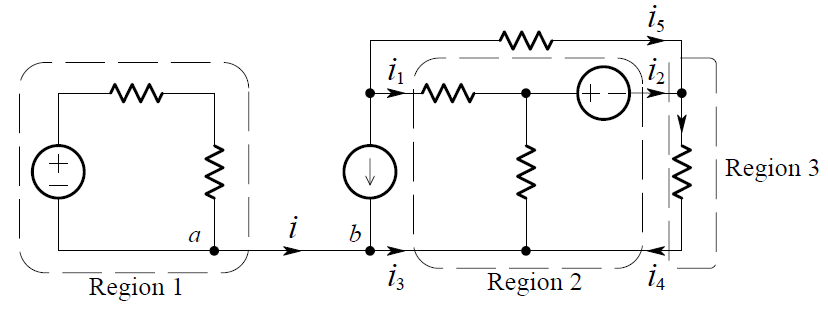
Applying KCL to Region 1, we get:
i = 0
For Region 2:
i1 + i3 + i4 = i2
For Region 3:
i2 + i5 = i4
You may now ask, “Since there is no current from point a to point b (or vice versa) why is the connection (a short-circuit) between the points there?” If the connection between the two points is removed, two separate circuits result. The voltages and currents within each individual circuit remain the same as before. Having the connection present constrains points a and b to be the same node, and hence be at the same voltage. It also indicates that the two separate portions are physically connected (even though there is no current between them).
