The Short-Circuit
Consider a resistor whose value is zero ohms. An equivalent representation of such a resistance, called a short-circuit, is shown below:
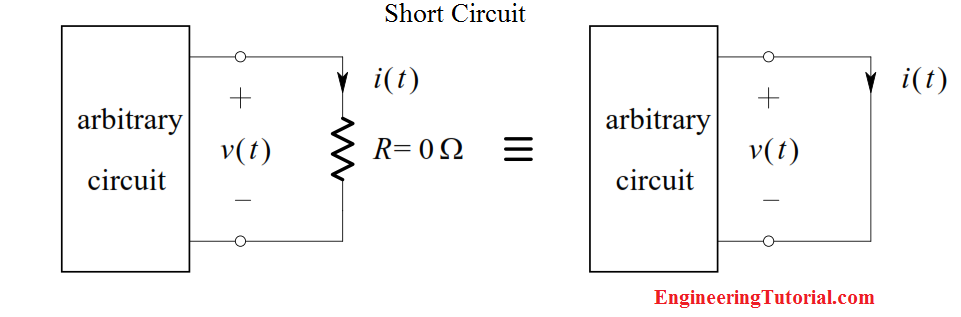
By Ohm’s Law: ( For short Circuit, R = 0 )
v = Ri = 0i = 0 V
Thus, no matter what finite value i(t ) has, v(t ) will be zero. Hence, we see that a zero-ohm resistor is equivalent to an ideal voltage source whose value is zero volts, provided that the current through it is finite.
The Open-Circuit
Consider a resistor having infinite resistance. An equivalent representation of such a resistance, called an open-circuit, is shown below:
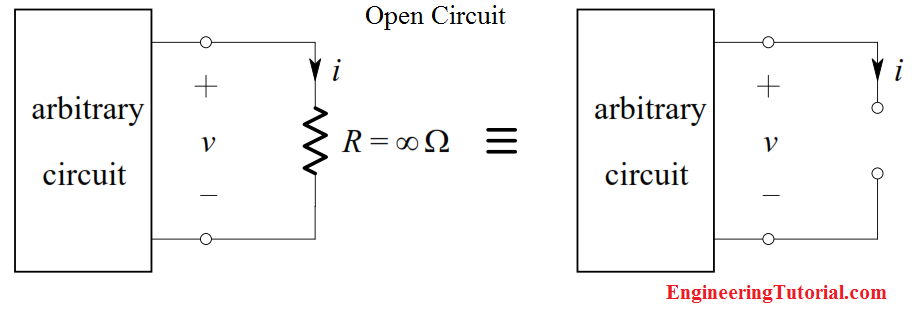
By Ohm’s Law: ( For short Circuit, R = ∞ )
i = v/R = v/∞ = ∞ A
Thus, no matter what finite value v(t ) has, i(t ) will be zero. Thus, we may conclude that an infinite resistance is equivalent to an ideal current source whose value is zero amperes, provided that the voltage across it is finite